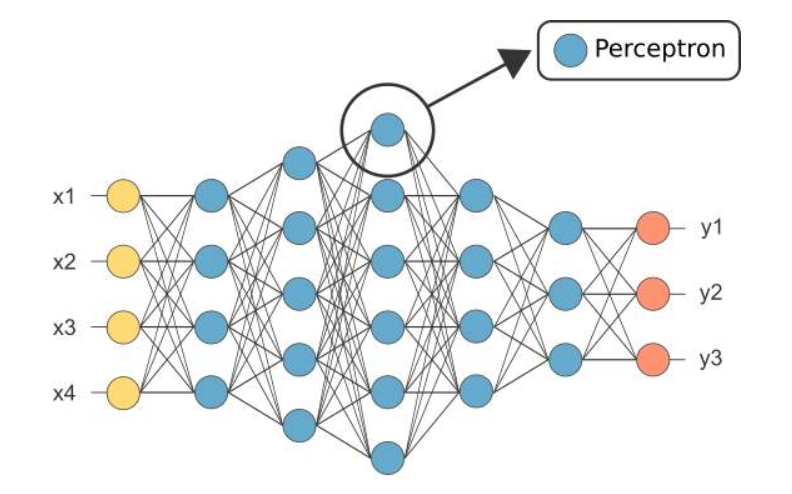
原理解读
MLP(Multi-Layer Perceptron):多层感知机**本质上是一种全连接的深度神经网络(DNN)**,感知机只有一层功能神经元进行学习和训练,其能力非常有限,难以解决非线性可分的问题。为了解决这个问题,需要考虑使用多层神经元进行学习。
核心思想
反向传播(BP, BackPropagation)
神经网络的学习过程可真是太牛B了,人类的学习过程是,从小学到大学,学习知识以后,都需要考试,然后根据得分修正以往的错误部分。BP的思想也是一样,一开始神经网络什么都不知道,给予网络随机的权重,然后进行学习,每次得到一个结果,我们将其与标准结果进行对比(这类似于考试成绩与标准答案进行对比)。然后根据差异寻找问题的根源。
BP算法基于梯度下降策略,以目标的负梯度方向对参数进行调整。
下面我举一个简单的例子,小伙伴们就可以清晰的知道BP的原理。
假设有N个样本,样本的特征数为F,因此输入矩阵的大小为[F, N],只有一个隐藏层,且神经元的个数为F1,因此w1的大小为[F1, F],b1的大小为[F, 1],经过计算后z1的大小为[F1, N],激活函数为ReLu,第一层的输出a1的大小为[F1, N],对于一个二分类问题,输出神经元的个数为1,因此w2的大小为[1, F1],b2的大小为[1, 1],经过计算后z2的大小为[1, N],激活函数为Sigmoid,第二层的输出$\hat{y}$的大小为[1, N]。
我们使用以下记号表示前向计算过程
$$z1 = w1 \cdot x + b1$$
$$a1 = ReLu(z1)$$
$$z2 = w2 \cdot a1 + b2$$
$$\hat{y} = Sigmoid(z2)$$
$$J(\hat{y}, y) = -[y \cdot log(\hat{y}) + (1 - y) \cdot log(1 - \hat{y})]$$
下面推导误差反向传播过程,我们只要计算出各个参数的梯度即可
$$\frac{\partial J}{\partial \hat{y}} = -(\frac{y}{\hat{y}} - \frac{1 - y}{1 - \hat{y}})$$
$$\frac{\partial J}{\partial z2} = \frac{\partial J}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z2} = -(\frac{y}{\hat{y}} \hat{y}(1 - \hat{y}) - \frac{1 - y}{1 - \hat{y}} \hat{y}(1 - \hat{y})) = \hat{y} - y$$
$$\frac{\partial J}{\partial w2} = \frac{\partial J}{\partial z2} \cdot \frac{\partial z2}{\partial w2} = \frac{\partial J}{\partial z2} \cdot a2^T$$
$$\frac{\partial J}{\partial b2} = \frac{\partial J}{\partial z2} \cdot \frac{\partial z2}{\partial b2} = \frac{1}{N}\sum_{1}^{N}\frac{\partial J}{\partial z2}$$
$$\frac{\partial J}{\partial a1} = \frac{\partial J}{\partial z2} \cdot \frac{\partial z2}{\partial a1} = w2^T \cdot \frac{\partial J}{\partial z2}$$
$$\frac{\partial J}{\partial z1} = \frac{\partial J}{\partial a1} \cdot \frac{\partial a1}{\partial z1} = \frac{\partial J}{\partial a1} * dReLu(z1)$$
$$\frac{\partial J}{\partial w1} = \frac{\partial J}{\partial z1} \cdot \frac{\partial z1}{\partial w1} = \frac{\partial J}{\partial z1} \cdot a1^T$$
$$\frac{\partial J}{\partial b1} = \frac{\partial J}{\partial z1} \cdot \frac{\partial z1}{\partial b1} = \frac{1}{N}\sum_{1}^{N}\frac{\partial J}{\partial z1}$$
代码实战
mlp_train.m
1 | clear;clc; |
mlp_test.m
1 | clc;close all; |
实验结果
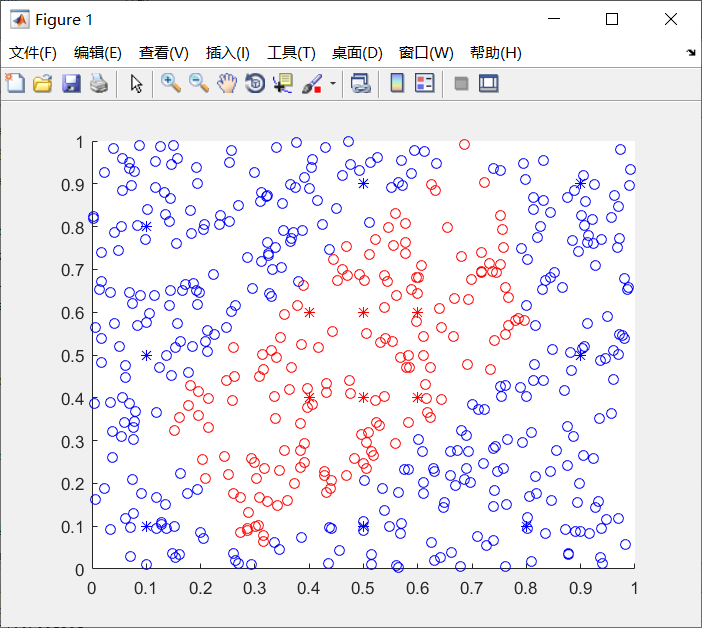
MLP(Multi-Layer Perceptron)优缺点
- 优点:
- 可以实现多分类任务。
- 参数量和迭代次数满足条件时,可以拟合线性不可分任务。
- 缺点:
- 计算量较大,训练时间较长。
- 算法可能陷入局部最优解,导致训练失败。